🎓 Leçon 1.2 — Distribution binomiale
📌 Objectifs
- Comprendre ce qu’est une distribution binomiale
- Savoir identifier une situation binomiale
- Savoir calculer une probabilité binomiale
1. 🔍 Définition
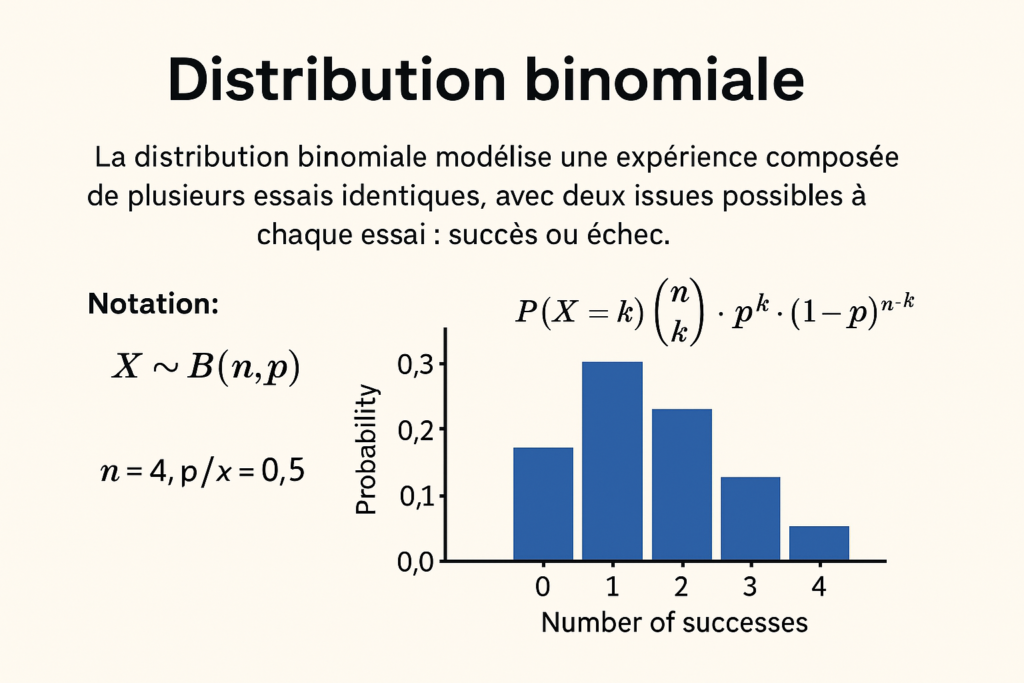
La distribution binomiale modélise une expérience composée de plusieurs essais identiques, avec deux issues possibles à chaque essai : succès ou échec.
Exemple :
Lancer une pièce 5 fois et compter le nombre de fois où l’on obtient « pile ».
Lancer une pièce 5 fois et compter le nombre de fois où l’on obtient « pile ».
2. 🎯 Conditions d’une loi binomiale
Une variable aléatoire suit une loi binomiale si :
- Il y a n essais indépendants
- Chaque essai a seulement deux issues : succès (probabilité p) ou échec (1 − p)
- La probabilité p est constante à chaque essai
3. 📐 Notation
Si la variable aléatoire X suit une loi binomiale, on écrit :
X ∼ B(n, p)
n : nombre d’essais
p : probabilité de succès à un essai
4. 🧮 Formule de probabilité
P(X = k) = C(n, k) × pk × (1 − p)n − k
k : nombre de succès recherchés
C(n, k) : coefficient binomial (ou combinatoire)
Exemple :
Quelle est la probabilité d’obtenir exactement 2 « pile » en 4 lancers de pièce (p = 0,5) ?
P(X = 2) = C(4, 2) × (0,5)² × (0,5)² = 6 × 0,25 × 0,25 = 0,375
5. ✅ À retenir
- La loi binomiale s’applique aux comptages de succès
- Elle est discrète (valeurs entières de 0 à n)
- Le maximum de probabilité est souvent autour de np
