-
Table des matières
-
-
-
-
-
-
-
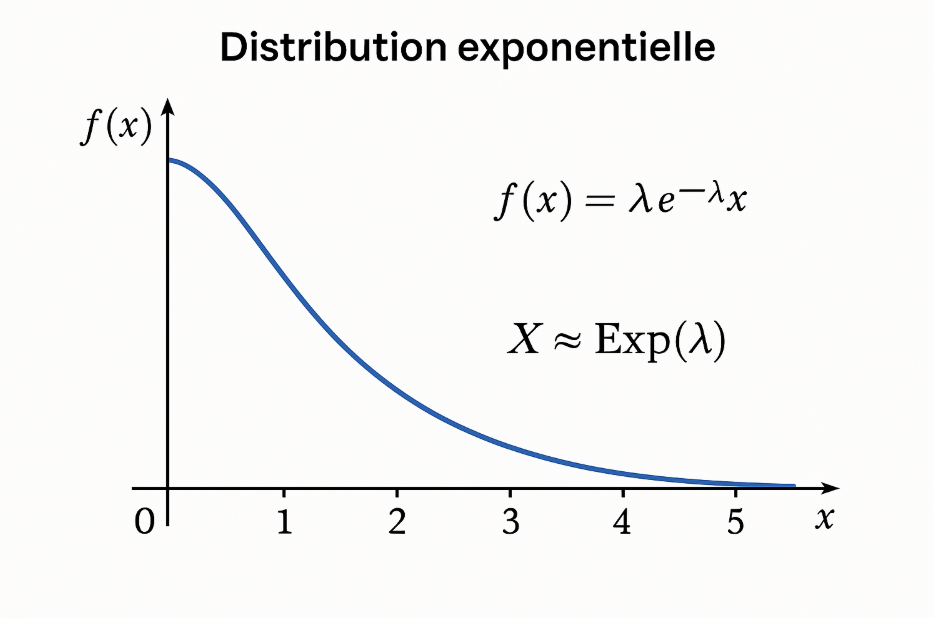
La distribution exponentielle modélise le temps d’attente entre deux événements successifs dans un processus aléatoire et continu, à un taux constant.
λ (lambda) : taux d’occurrence par unité de temps
➤ Plus λ est grand, plus les événements sont fréquents.
➤ Densité décroissante : forte probabilité pour les petits temps d’attente.