-
Table des matières
-
-
-
-
-
-
-
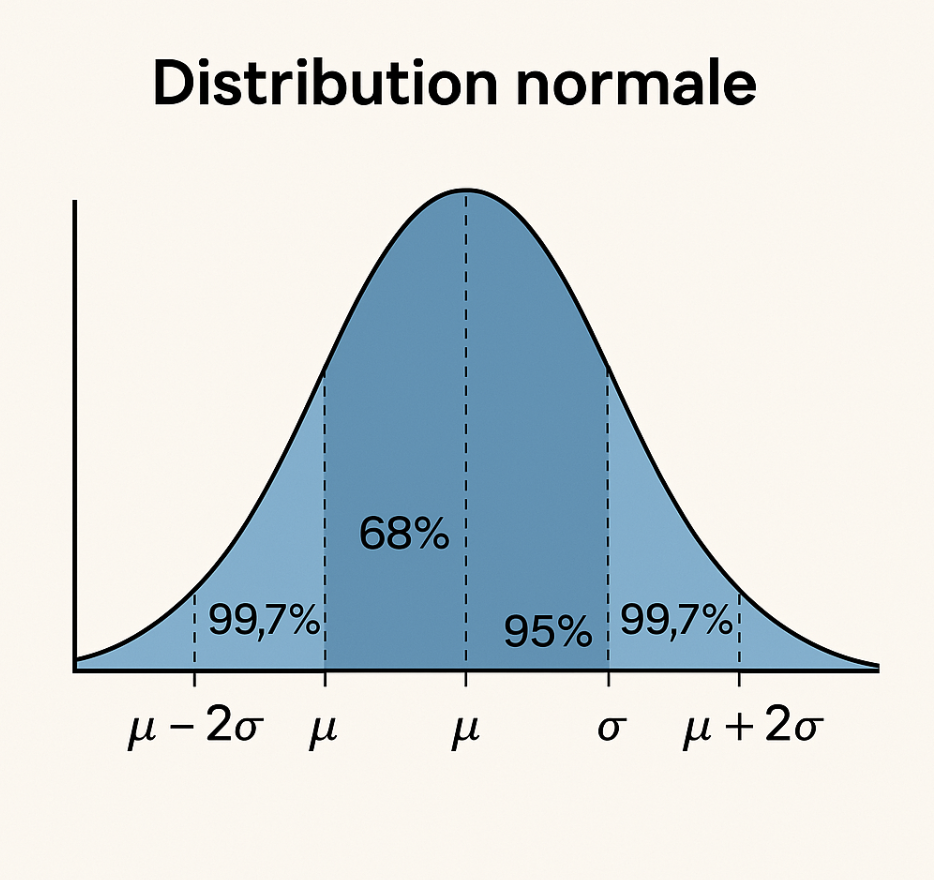
La distribution normale (ou loi de Gauss) modélise des phénomènes où les valeurs sont réparties symétriquement autour d’une moyenne.
μ : moyenne
σ² : variance (σ = écart type)
➤ La courbe est en cloche, symétrique autour de μ
Pour faciliter les calculs, on standardise avec la variable Z :
On peut ensuite utiliser des tables de Z (loi normale centrée réduite) pour retrouver les probabilités.